A Preliminary Study on the Separation of Natural and Synthetic Emeralds Using Vibrational Spectroscopy
ABSTRACT
More than 300 natural and synthetic emeralds from various sources were examined with Raman spectroscopy. Of this set, 36 KBr pellets of different samples were also examined with FTIR spectroscopy. In many cases, the presence or absence of specific Raman and FTIR bands, and the exact position of apparent maxima, are correlated to the weight percentage of silicon and/or alkali. This can help determine whether an emerald is natural or synthetic.
INTRODUCTION
Both vibrational Raman and FTIR spectroscopy have been widely applied in identifying synthetic and natural beryl (Wood and Nassau, 1968; Schmetzer and Kiefert, 1990; Huong et al., 2010). These methods are used to characterize the water molecules present in the beryl channel sites, known as type I and type II water molecules. Type I water molecules occur independently of alkalis, while type II are associated with nearby alkalis. In most natural beryl, Raman bands arising from both types are visible, though some natural beryls with relatively low alkali present weak type II–related bands. Most hydrothermal synthetic samples display the Raman signal of type I water (the type II signal is barely visible in most cases). Neither band is visible in flux-grown synthetic beryl, which has no water in its structure (Schmetzer and Kiefert, 1990). These methods are not effective in cases such as relatively low-alkali natural beryl, where the type I water band is observed almost exclusively (Huong et al., 2011), and some hydrothermal synthetic beryl that contains a small amount of alkalis and can show a weak type II water Raman signal as well.
This article presents some additional differences that could be used to distinguish between natural and synthetic emeralds. These features, mostly generated by silicon- and/or alkali-related vibrations, include a Raman band at about 1070 cm–1 (Adams and Gardner, 1974) and an FTIR band around 1200 cm–1 (Aurisicchio et al., 1994) and its shoulder at about 1140 cm–1.
BACKGROUND
Beryl—Be3Al2Si6O18—has a structure composed of six-membered rings of [SiO4]4– tetrahedra. The silicate rings are aligned precisely over one another, forming open channels parallel to the c-axis of the crystal (Huong et al., 2010). The diameter of the channels has the capacity to hold large ions and molecules such as alkalis (Na+, K+) and water (Goldman et al., 1978; Aines and Rossman, 1984). Alkalis act as charge compensators for the substitution of main elements such as Al3+ and Be2+. The ideal composition of the main elements to match the exact stoichiometry of beryl is 67.0 wt.% SiO2, 18.9 wt.% Al2O3, and 14.1 wt.% BeO. In beryl, Al3+ in octahedral sites and Be2+ in tetrahedral sites are commonly substituted with other elements including Cr3+, V3+, Fe3+, Fe2+, Mg2+, Mn2+, Be2+, and Li+. Additionally, charge compensation by alkalis (including Cs, Rb, K, and Na) and water in the ring channels diminishes the weight % of Si in the formula. These additions affect the silicon-related vibrational signals.

Because growers of synthetic beryl follow the exact stoichiometric formula, unlike nature, some differences in silicon-related vibrations would be expected. Therefore, Raman and FTIR spectroscopy could provide valuable information for assessing the origin of emeralds (figure 1).
MATERIAL AND METHODS
We collected 326 natural and synthetic emerald samples for Raman analysis. The natural samples consisted of 260 crystals obtained directly from mines in Brazil (20 from Santa Terezinha and 15 each from Carnaíba, Capoeirana, Itabira, and Socotó); Colombia (30 from Chivor); Austria (10 from Habachtal); Russia (10 from the Ural Mountains); Madagascar (30 from Mananjary); South Africa (30 from Transvaal); Zambia (30 from Kafubu); Nigeria (30 from Gwantu); and China (10 from Malipo). The 66 faceted synthetic emeralds consisted of hydrothermally grown (15 Tairus and 10 Biron) and flux-grown (20 Gilson, 20 Chatham, and 1 Lennix) samples provided by the producers.
Raman spectra from 200 to 1200 cm–1 were collected with a Jobin Yvon (Horiba) LabRam HR 800 spectrometer equipped with an Olympus BX41 optical microscope and a Si-based CCD (charge-coupled device) detector. All samples (except the faceted ones) were polished on two sides, oriented parallel to the c-axis. They were polished with corundum paste to obtain a smooth surface and ultrasonically cleaned with acetone. The instrumentation used an Ar+ ion laser (514 nm emission), a grating with 1800 grooves/mm, and a slit width of 100 mm. These parameters, and the optical path length of the spectrometer, yielded a spectral resolution of 0.8 cm–1. The spectral acquisition time was set at 240 seconds for all measurements, and sample orientation was carefully controlled. The electric vector of the polarized laser beam was always parallel to the c-axis.
For FTIR measurements, we chose 36 samples (27 natural emeralds from various sources and 9 synthetics from different producers; see table 1). FTIR spectra were recorded in the 400–1400 cm–1 range by a PerkinElmer 1725X FTIR spectrometer with 100 scans and 4 cm–1 spectral resolution using the KBr pellet method (2 mg of powder drilled from each sample mixed with 200 mg of KBr). Peak analysis of both Raman and FTIR results was performed with an OriginLab Origin 7.5 professional software package, and the peaks were fitted using a Gauss-Lorentz function.
| TABLE 1. Chemical data of natural and synthetic emeralds by electron microprobe (silicon content) and LA-ICP-MS (alkali content). | ||
| Source |
Silicon
(wt.%)
|
Total alkalis
Li+Na+K+Rb+Cs(wt.%)
|
| Natural | ||
| Colombia/Chivor 1 | 65.272±0.333 | 0.330±0.024 |
| Colombia/Chivor 2 | 66.134±0.081 | 0.355±0.030 |
| Colombia/Chivor 3 | 65.609±0.392 | 0.521±0.041 |
| Colombia/Chivor 4 | 65.921±0.312 | 0.683±0.031 |
| Colombia/Chivor 5 | 65.306±0.284 | 0.405±0.053 |
| Nigeria/Gwantu 1 | 66.254±0.168 | 0.208±0.021 |
| Nigeria/Gwantu 2 | 66.188±0.056 | 0.142±0.018 |
| Nigeria/Gwantu 3 | 64.986±0.409 | 0.230±0.041 |
| Nigeria/Gwantu 4 | 65.755±0.220 | 0.208±0.035 |
| Nigeria/Gwantu 5 | 65.820±0.081 | 0.238±0.052 |
| China/Malipo 1 | 63.521±0.302 | 0.966±0.062 |
| China/Malipo 2 | 63.914±0.472 | 1.116±0.036 |
| Brazil/Santa Terezinha | 63.245±0.221 | 1.591±0.041 |
| Brazil/Socotó | 64.306±0.162 | 1.809±0.032 |
| Brazil/Capoeirana | 64.109±0.093 | 1.657±0.081 |
| Brazil/Carnaíba | 64.287±0.178 | 1.819±0.032 |
| Brazil/Itabira | 63.410±0.254 | 0.914±0.011 |
| Russia/Ural 1 | 63.823±0.213 | 1.760±0.070 |
| Russia/Ural 2 | 64.521±0.243 | 1.850±0.021 |
| Austria/Habachtal 1 | 64.470±0.151 | 1.567±0.072 |
| Austria/Habachtal 2 | 62.719±0.083 | 1.585±0.045 |
| Madagascar/Mananjary 1 | 63.554±0.412 | 1.116±0.017 |
| Madagascar/Mananjary 2 | 64.209±0.244 | 1.629±0.029 |
| Zambia/Kafubu 1 | 64.228±0.109 | 1.552±0.006 |
| Zambia/Kafubu 2 | 63.523±0.372 | 1.611±0.012 |
| South Africa/Transvaal 1 | 63.723±0.251 | 1.701±0.017 |
| South Africa/Transvaal 2 | 63.178±0.222 | 1.872±0.045 |
| Synthetic (hydrothermal) | ||
| Biron 1 | 66.710±0.360 | 0.166±0.011 |
| Biron 2 | 66.650±0.163 | 0.142±0.014 |
| Tairus 1 | 66.489±0.214 | 0.067±0.009 |
| Tairus 2 | 66.783±0.202 | 0.052±0.014 |
| Synthetic (flux) | ||
| Gilson 1 | 66.391±0.101 | 0.041±0.003 |
| Gilson 2 | 66.524±0.323 | 0.049±0.010 |
| Chatham 1 | 66.830±0.272 | 0.171±0.019 |
| Chatham 2 | 66.591±0.130 | 0.112±0.012 |
| Lennix 1 | 66.233±0.164 | 0.033±0.005 |
Chemical analysis of the same 36 samples was carried out with electron microprobe for Si and laser ablation–inductively coupled plasma–mass spectrometry (LA-ICP-MS) for all other elements studied. Microprobe analyses were performed with a JEOL JXA 8900RL instrument equipped with wavelength-dispersive spectrometers, using 20 kV acceleration voltage and a 20 nA filament current. Silicon was analyzed by microprobe, with wollastonite used as the standard. For most elements, including silicon, the detection limit for wavelength-dispersive (WD) spectrometers is between 30 and 300 parts per million (ppm). The precision depends on the number of X-ray counts from the standard and sample and the reproducibility of the WD spectrometer mechanisms. The highest obtainable precision is about 0.5%.
LA-ICP-MS quantitative analysis for all elements except Si (including Li, Be, B, Na, Mg, Al, P, K, Ca, Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Ga, Ge, Rb, Sr, Y, Zr, Nb, Mo, Cs, Ba, La, and Ta) was conducted using an Agilent 7500ce ICP-MS in pulse-counting mode. Ablation was performed with a New Wave Research UP-213 Nd:YAG laser ablation system, using a pulse repetition rate of 10 Hz, an ablation time of 60 seconds, a dwell time of 10 milliseconds per isotope, a 100 µm crater diameter, and five laser spots averaged for each sample. Silicon (determined with the microprobe) was used as the internal standard. Data reduction was carried out using Glitter software. The amount of material ablated in laser sampling varied in each spot analysis. Consequently, the detection limits were different for each spot and were calculated for each acquisition. Detection limits for the analyzed elements ranged between 0.0001 and 0.5 ppm. For trace elements such as Ta, La, Nb, and Y, the detection limit was 0.0001 ppm. The detection limit was 0.01 ppm for minor elements such as alkalis and 0.5 ppm for main elements, including Be and Al. Analyses were calibrated using the NIST 612 glass standard. BCR-2G glass was also measured as a reference material.
RESULTS AND DISCUSSION
The Raman Peak at Approximately 1070 cm–1. Earlier studies attributed this peak to either Si-O stretching (e.g., Adams and Gardner, 1974; Charoy et al., 1996) or Be-O stretching in the beryl structure (e.g., Kim et al., 1995; Moroz et al., 2000). Recent results have shown that this peak is mainly due to Si-O stretching (Huong, 2008).
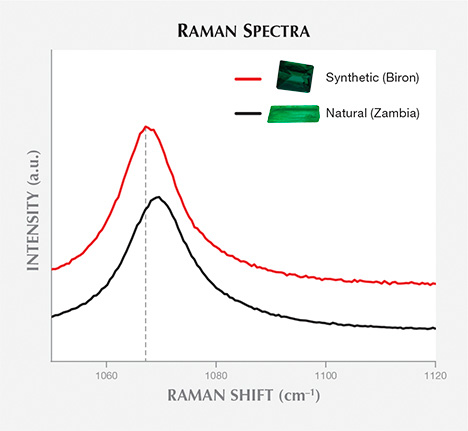
Figure 2 presents Raman spectra from 1050 to 1120 cm–1 for a hydrothermal synthetic emerald (Biron) and a natural emerald (Kafubu, Zambia). The exact position and shape of the observed peaks differ. For the synthetic sample, the apparent maximum is situated at around 1067.5 cm–1, with a full width at half maximum (FWHM) of 12 cm–1. The apparent maximum for the synthetic samples is positioned at 1067.0–1068.0 cm–1, and the FWHM varies between 11 and 14 cm–1. There is no variation between the different growth methods (hydrothermal vs. flux) or manufacturers regarding this peak (figure 3). The natural sample presented in figure 2 shows an apparent maximum at approximately 1070 cm–1 and a FWHM of 18 cm–1. In the natural samples, the apparent maximum ranged from 1068 to 1072 cm–1 and FWHM varied between 12 and 26 cm–1 (with no clear difference among geographic origins; figure 3). The variation in the exact position (shifting) and shape (broadening) of this peak is probably due to the presence of at least two different bands; the peak’s position and shape are linked to the relative intensities of these bands. Peak position and FWHM show overlap between some natural and synthetic samples (when the apparent maxima overlap at 1068 cm–1 and the FWHM at 12–14 cm–1). Thus, only the natural samples have presented peak maxima above 1068 cm–1 with a FWHM 15 cm–1, and only synthetic emeralds have maxima at 1067 cm–1 with a FWHM of 11 cm–1. When they are not within overlap ranges, peak position and FWHM can help identify natural and synthetic emerald.
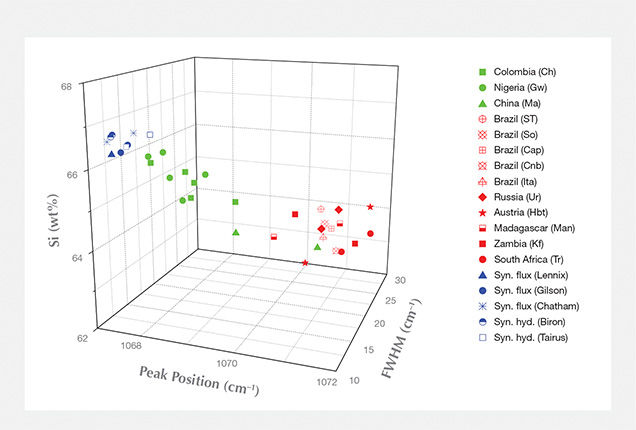
Correlation diagrams of chemical composition data, 1070 cm–1 Si-related Raman peak positions, and FWHMs showed that the Si-O band broadened and shifted to higher wavenumbers when the Si wt.% decreased (figure 3). The shifting and broadening of the peak probably result from chemical substitution.
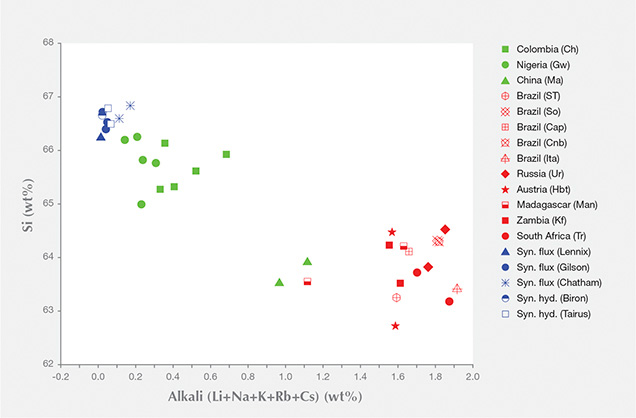
In figure 4, the correlation between Si and alkali ion weight percentages is observed; samples with lower than stoichiometric Si show high alkali wt.%. As silicon is the main element in the beryl structure, only a relatively significant decrease of silicon wt.% (i.e., a relatively significant increase of alkali wt.%) causes a detectable change in the Raman band properties. When the wt.% of silicon (as well as the sum of alkalis) is significantly different (for example, up to 3 wt.% variance between natural and synthetic samples), the difference in band properties can be observed. When the silicon wt.% is more similar (around 1 wt.% variance among natural samples; i.e., “low” alkali wt.%), the difference in band properties is not visible. In “high-alkali” emeralds (1.5% alkali content), this band shifts at about 1069–1072 cm–1 (FWHM of 16–26 cm–1). In “low-alkali” emeralds with 0.5% alkali content (e.g., Nigerian and Colombian) and in synthetic samples with 1.5% alkali content, these bands shift at about 1068–1070 cm–1 (FWHM of 12–18 cm–1) and 1067–1068 cm–1 (FWHM of 11–14 cm–1), respectively.
The 1200 cm–1 FTIR Absorption Band and Its Shoulder. This band was attributed to Si-O stretching in the beryl structure (Aurisicchio et al., 1994). Figure 5 presents the FTIR absorption spectra of a synthetic emerald (flux-grown, Gilson) and a natural emerald (Ural Mountains, Russia) from 400 to 1600 cm–1 (see inset from 1100 to 1300 cm–1).
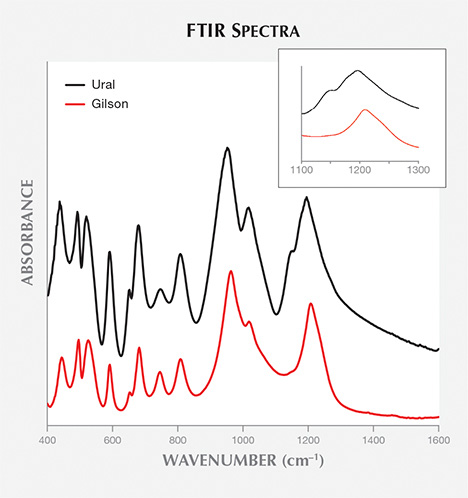
All synthetic samples showed an apparent maximum at around 1200 to 1207 cm–1, while natural emeralds showed an apparent maximum at about 1171 to 1203 cm–1. This peak appears to consist of more than one band, and its exact position and shape are linked to the relative intensities of these bands. An overlap of the apparent maxima was observed with some low-alkali natural and synthetic samples from 1200 to 1203 cm–1. In addition, all high-alkali emeralds displayed a shoulder at about 1140 cm–1. The shoulder has not been reported in previous studies. Among low-alkali samples, this shoulder could be seen in Colombian samples (Chivor) but not in Nigerian emeralds. Its exact position is also linked to the main peak position. The shoulder was not observed in any of the synthetic samples (again, see figure 5).
Correlating chemical data showed that the presence of the shoulder was also related to alkali content. In the samples with high alkali ion content, the shoulder at 1140 cm–1 was distinct. Moreover, the apparent maximum of the peak at 1200 cm–1 shifted to lower wavenumbers. In samples with low alkali content, particularly synthetic samples, the shoulder disappeared and the apparent maximum at 1200 cm–1 shifted toward higher wavenumbers.
CONCLUSION
Natural and synthetic emeralds can sometimes be distinguished by the apparent maxima and FWHM of the silicon- and alkali-related Raman peak at 1070 cm–1. Using FTIR spectroscopy on KBr pellets of powdered samples, the distinction can sometimes be made based on the silicon-related peak at 1200 cm–1, as well as a shoulder, possibly linked to alkali content. Synthetic samples showed the Raman peak with apparent maxima from 1067 to 1068 cm–1 (FWHM of 11–14 cm–1) and FTIR apparent maxima from 1200 to 1207 cm–1. In natural emeralds, the Raman band displayed the band in the same range, but with apparent maxima from 1068 to 1072 cm–1, FWHM varying between 12 and 26 cm–1, and the FTIR band positioned from 1171 to 1203 cm–1. All natural samples with high alkali content display a shoulder at 1140 cm–1, while synthetic emeralds do not. Low-alkali natural samples from Colombia (Chivor) present this shoulder, but Nigerian emeralds do not. For more precise conclusions, a larger number of samples—namely synthetics with higher alkali content (0.2%) and natural emeralds with lower alkali (0.2%)—must be investigated.



