Pleochroism in Faceted Gems: An Introduction

ABSTRACT
While virtually all gemological texts cover pleochroism, it is almost always related to viewing with a dichroscope. Exactly how pleochroism manifests itself in faceted gems is largely ignored. This article discusses this phenomenon in doubly refractive gemstones, specifically as it relates to overall color appearance in faceted gems. Contrary to popular belief, pleochroism can be visible in faceted gems even when they are cut with an optic axis parallel to the direction of view.
INTRODUCTION
In describing colored gemstones, the major factors influencing color are hue (position of a color on a color wheel), lightness (tone), saturation (intensity), color zoning, metamerism (color-change), dispersion, and pleochroism. This article deals with the last of these properties. The term pleochroism (from the Greek “pleio,” many, and “chros,” color) describes a variation of color with direction in doubly refractive gems (figure 1). Virtually all gemological texts note this effect and describe it in detail. Yet many of these descriptions deal only with the identification of this property. When lapidary aspects are discussed, the focus is on orientation, generally omitting mention of exactly how pleochroism affects the appearance of faceted stones. The purpose of this article is to provide a detailed description of pleochroism as it relates to the appearance of faceted gems.
INTRODUCTION TO OPTICAL CRYSTALLOGRAPHY
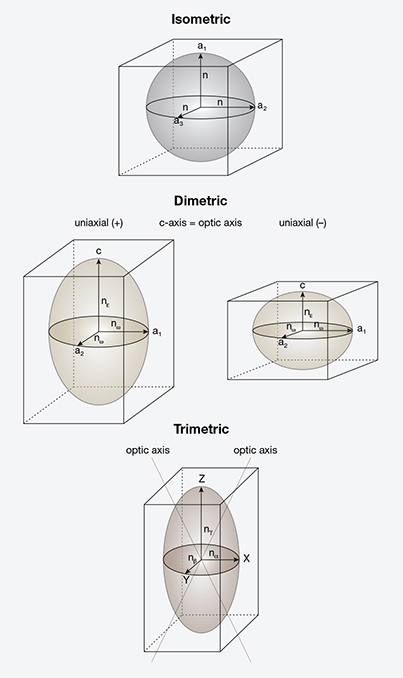
For gemological purposes, crystals can be divided into three optical groups based on their lattice symmetry: isometric, dimetric (uniaxial), and trimetric (biaxial); see table 1.
| TABLE 1. Optical crystallography simplified. | ||||
| Structure | Structure type | Optic character | Pleochroism | Examples |
| Amorphous | No order No axes |
Singly refractive | None | Amber, glass, opal |
| Isometric | One crystallographic axis length (cubic) a1 = a2 = a3 |
Singly refractive | None | Diamond, spinel, garnet |
| Dimetric (Uniaxial) |
Two crystallographic axis lengths a1 = a2 ≠ c (tetragonal) a1 = a2 = a3 ≠ c (hexagonal) |
Doubly refractive Uniaxial Two RIs (nω, nε), one optic axis |
May be dichroic | Corundum, tourmaline, zircon |
| Trimetric (Biaxial) |
Three crystallographic axis lengths a ≠ b ≠ c (orthorhombic, monoclinic, triclinic |
Doubly refractive Biaxial Three RIs (nα, nβ, nγ), two optic axes |
May be trichroic | Andalusite, iolite, topaz, zoisite, chrysoberyl |
Imagine a perfect sphere. If you draw a line from the center to the surface in any direction, all possible lines will have the same length. This sphere represents how light behaves in isometric crystals. Now if we stretch or compress that perfect sphere in a single direction, it becomes dimetric: a perfect circle when viewed in one direction, but oval when viewed at right angles to the direction of distortion. In other words, two of the three dimensions are equidistant, but the third is either stretched (positive uniaxial) or compressed (negative uniaxial).
Finally, if we distort our perfect sphere in not just one direction but two, we end up with a trimetric crystal, where each of the three dimensions has a different length (see figure 2).
Within singly refractive gem materials, the spacing of lattice points is essentially identical in all three mutually perpendicular dimensions (top to bottom, side to side, back to front). As a result, these materials transmit light in a manner that is independent of crystal orientation—light therefore moves through these crystals in all directions at a single speed and is permitted to vibrate in any direction perpendicular to the direction of travel.
This is not the case, however, in doubly refractive gems. All doubly refractive gems are anisotropic crystals, and the arrangement of their lattice points varies with direction. Uniaxial materials possess one unique optic axis (the c-axis) along which the orientation of lattice points differs from that of the other two crystal axes (the a-axes); with biaxial gems, the orientation differs along each of the three crystal axes (a-, b-, and c-axes). The result of this differing arrangement of lattice points in doubly refractive gems (as opposed to singly refractive gems) is that light traveling through these crystals is split into two separate paths or rays (with the exception of light waves traveling parallel to an optic axis), each traveling at a different speed and thus possessing a different refractive index (RI). For more on the behavior of light entering a crystal, see box A.
| Box A: Electromagnetic Radiation and Crystals |
| Visible light is one form of electromagnetic radiation. Light is sometimes described as behaving like a particle, but when dealing with transmission and reflection, it is more convenient to describe light as a wave (Frye, 1974). This is often referred to as the “dual nature of light.” For the purposes of pleochroism, the wave theory is more appropriate. Electromagnetic waves consist of electric (E) and magnetic (M) portions, each mutually perpendicular. The electric portion of the wave interacts with, and is altered by electrons, and so it is only the E portion of the wave that will be considered when referring to refraction and polarization (figure A-1). The electric vector (vibration) of ordinary light, such as sunlight, may extend in any direction perpendicular to the direction of travel (figure A-2). Such light is said to be unpolarized. Should the light wave be forced to vibrate in a single plane, the ray is polarized. When light enters a substance of greater optical density, it is slowed because the electron density is greater and thus there is greater interference with the E portion of the wave. If the electron density of that substance is random, such as in a gas or glass, the polarization is not affected. The same holds true when it enters isometric (cubic) crystals, where the lattice points are arranged identically in each of the three dimensions. In all other crystals, the lattice points (and thus the electron clouds) are unevenly spaced. The spacing of lattice points in dimetric crystals varies in two dimensions, while that of trimetric crystals varies in all three dimensions. This affects the manner in which light moves through them. Non-cubic crystals are termed anisotropic. They both split and perpendicularly polarize light upon entry, except in directions where the electron clouds are symmetrical. Those directions are termed optic axes, and light travels along these directions as it does in isotropic materials. When light enters an anisotropic substance in a direction not parallel to an optic axis, it splits into two segments, each of which is polarized perpendicular to the other. Polarization can also occur when light strikes a highly reflective surface, such as a lake, producing what our eyes perceive as glare. The direction of polarization is parallel to the reflective surface. If one dons “Polaroid” sunglasses, the glare is eliminated because the lenses contain tiny polarizers oriented perpendicular to the horizon. 
Figure A-1. Electromagnetic waves consist of two mutually perpendicular portions, an electric vector and a magnetic vector. The electric vector interacts with, and is altered by, electrons. This produces effects such as refraction and pleochroism. Illustration by Richard W. Hughes.
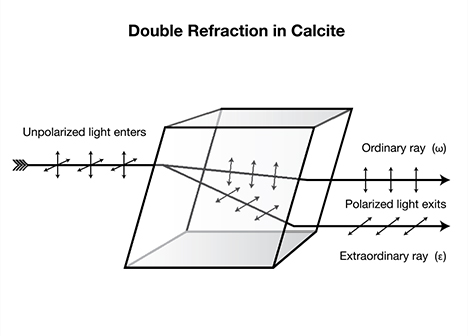
Figure A-2. When light enters a doubly refractive material in directions not along the optic axis, it is split into two portions, each polarized perpendicular to the other. Each ray may also be absorbed differently, resulting in pleochroism. Illustration by Richard W. Hughes.
|
Uniaxial gems possess two rays—the ordinary (o) and extraordinary (e) rays—and two RI values—omega (ω) and epsilon (ε), respectively. The o-ray always vibrates perpendicular to the c-axis, while the e-ray vibrates in a plane containing the c-axis. The vibrations of each ray are mutually perpendicular, and they vibrate roughly perpendicular to the direction of travel.
In biaxial gems, there are three different rays and three different RIs: alpha (α), beta (β), and gamma (γ), although only two are ever found in any one direction. The vibrations of alpha, beta, and gamma are parallel to the optical directions X, Y, and Z, respectively. Although the three crystallographic axes of biaxial minerals are not always mutually perpendicular, X, Y, and Z are always mutually perpendicular.
Uniaxial gems contain one optic axis (the direction of single refraction), which is parallel to the c-axis; biaxial gems contain two optic axes (two directions of single refraction), which lie in the X-Z plane. The major vibration directions of both uniaxial and biaxial gems are shown in figure 2.
Because each polarized light ray in a doubly refractive gem is vibrating across a slightly different arrangement of lattice points, each ray is absorbed differently. In many cases, the difference in absorption between one ray and another is too slight to detect with the eye, or even with a dichroscope. Where the differences are large enough, one observes a variation in color with viewing direction. Such variations are known as pleochroism, and they are most distinct in deeply colored specimens of the same gem species.
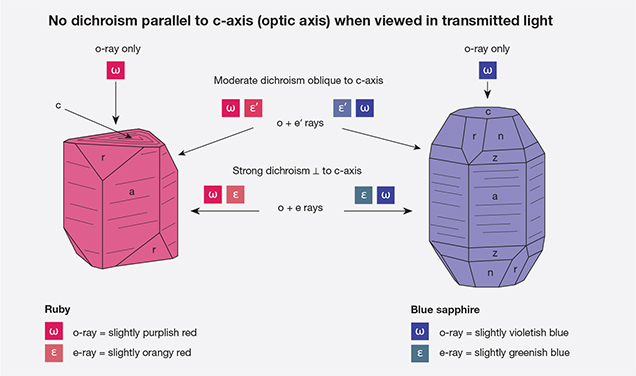
Uniaxial gems possess two different vibration directions—omega (ω) and epsilon (ε)—and may therefore exhibit two different colors (dichroism). Biaxial gems possess three different vibration directions—alpha (α), beta (β), and gamma (γ)—and so may show three different colors (trichroism), but only two in any single direction. Blue sapphire and tourmaline are strongly dichroic uniaxial gems, while tanzanite (again, see figure 1) provides an example of a strongly trichroic biaxial stone. Not all uniaxial gems display visible dichroism, however, and not all biaxial gems display visible trichroism. Some uniaxial gems show only one color, and biaxial gems may show only one or two colors.
When viewed in transmitted light with a dichroscope, pleochroism in uniaxial stones varies in the following ways, as shown in figure 3:
- Parallel to the c-axis, only the ordinary ray is seen. As a result, there is no pleochroism.
- At right angles to the c-axis, both the ordinary and extraordinary rays are seen; this position shows the strongest dichroism.
- At angles oblique to the c axis, the ordinary ray is seen; the second color (usually referred to as ε′) diverges from that of the o-ray as one moves away from the c-axis.
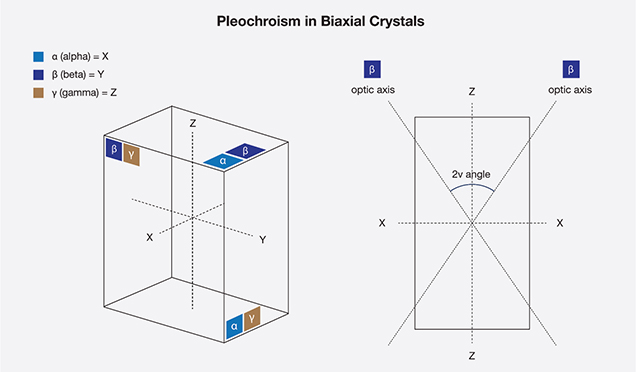
With biaxial stones, the situation is similar but slightly more complex. Light traveling along the Z direction will vibrate parallel to X and Y, so the two colors seen with a dichroscope will be those of alpha (X) and beta (Y). Light traveling along the X direction will vibrate across Y and Z, so the two colors seen will be those of beta (Y) and gamma (Z). When light travels parallel to Y, it vibrates along X and Z; the colors seen are those of alpha (X) and gamma (Z). Should light travel parallel to either of the two optic axes in a biaxial stone, only one color will be seen, that of beta (figure 4).
PLEOCHROISM IN FACETED UNIAXIAL GEMS
Let’s examine how this applies to the appearance of faceted stones. Figure 5* shows a uniaxial gem cut with the c-axis perpendicular to the table facet (since the crown plays only a minor role in the pleochroism of a faceted stone, it will be eliminated from this discussion for simplicity’s sake). Suppose the stone is a perfect square cut with only four pavilion facets (marked N, S, E, and W for north, south, east, and west). The a-axes are contained in the horizontal plane.
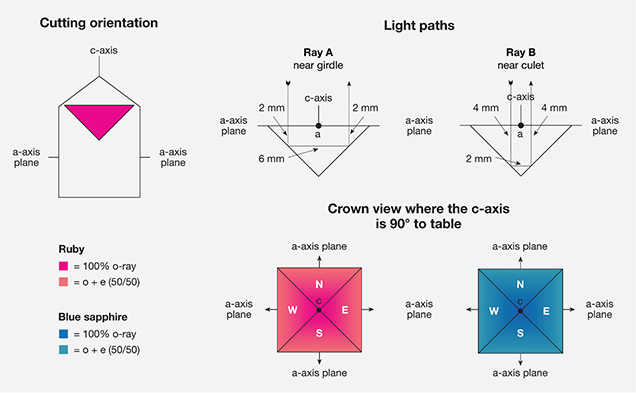
For light entering the stone parallel to the c-axis, only the o-ray would be obtained. When the light strikes facet W, however, the direction is changed. It then travels in the plane of the a-axes, giving an equal mixture of o- and e-rays. Upon striking facet E, the direction is again changed, causing the ray to exit the stone parallel to the c-axis. This again produces the o-ray only for this portion of its journey. Should the ray strike facets N or S instead, this still would not alter the above combinations.
At first it might seem that uniaxial stones cut with the c-axis perpendicular to the girdle plane would show one uniform color across their face. This is not the case, however, because the facet arrangement causes light to change direction during its journey through the gem. In uniaxial gems where the o-ray is more intensely colored than the e-ray, the color will appear slightly less intense near the girdle than near the culet, because the percentage of e-ray mixed into the color increases as light approaches the girdle.
In figure 5, the gem has a girdle diameter of 10 mm and a pavilion angle of 45°, and the c-axis is cut perpendicular to the table plane.
- Ray A enters near the girdle, traveling 4 mm parallel to the c-axis (o-ray only) and 6 mm parallel to the a-axis (3 mm of o-ray and 3 mm of e-ray). The color of Ray A therefore consists of 70% o-ray and 30% e-ray.
- Ray B strikes the pavilion much closer to the culet. Ray A and Ray B have identical path length, each traveling 10 mm through the gem. But Ray B’s light path consists of 8 mm parallel to the c-axis (8 mm of o-ray only) and just 2 mm parallel to the a-axis (1 mm of o-ray and 1 mm of e-ray). Thus, the color of Ray B is 90% o-ray and only 10% e-ray.
The conclusion is that when a uniaxial gem is cut with the c-axis perpendicular to the table facet, there can still be visible pleochroism. The o-ray color is stronger at the culet, gradually diminishing toward the girdle. To the best of the author’s knowledge, this fact has not been described in the gemological literature.
In uniaxial gems such as blue zircon, ruby, blue sapphire, and tourmaline, where the e-ray is less saturated in color than the o-ray, the color near the girdle will appear slightly less saturated because it has a higher percentage of e-ray mixed into the color. With gems such as blue benitoite, where the e-ray is more intensely colored than the o-ray, the reverse would hold true. The color would be lightest at the culet, darkening toward the girdle. Since making this discovery, the author has found that such differences are subtle at best, and in many cases undetectable to the unaided eye. In large, strongly pleochroic stones, however, the effect can be striking.
Now let us consider a uniaxial gem cut with the c-axis parallel to the table rather than perpendicular (figure 6):
- Ray A has 6 mm of o-ray only, and 4 mm of equally mixed o- and e-rays, giving a total of 80% o-ray and 20% e-ray.
- Ray B consists of 2 mm of o-ray only, and 8 mm of equally mixed o- and e-rays, giving a total of 40% o-ray and 60% e-ray. As a result, the color on these facets will show more of the o-ray near the girdle and less at the culet.
- Rays C and D are equal mixtures of o- and e-rays because their entire journey takes place perpendicular to the c-axis. Those facets will display a uniform 50%–50% split.
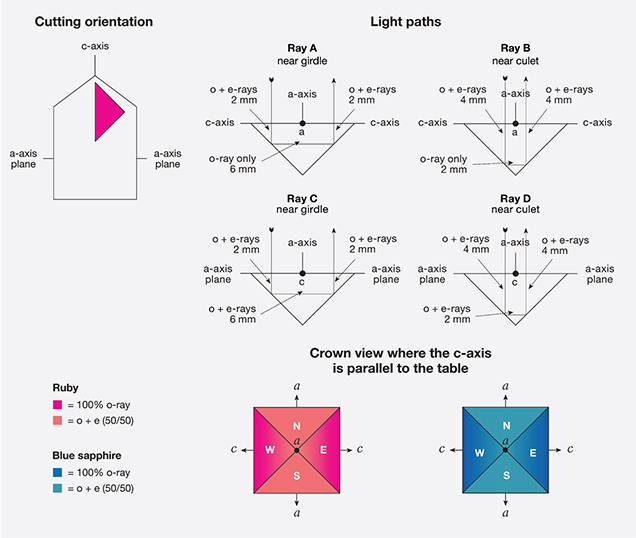
In summary, when pleochroic gems are cut with the c-axis parallel to the table facet, a pleochroic “bow tie” can be seen, as shown at the bottom of figure 6. A striking example of these differences in color due to pleochroism is found in the first edition of Joel Arem’s Color Encyclopedia of Gemstones (1977). Color plate 64 shows a round 15.6 ct Cambodian blue zircon (uniaxial) that has been cut with the c-axis parallel to the table facet (figure 7). In blue zircon, the o-ray is blue while the e-ray is colorless. This orientation has resulted in a large white “bow tie” that is obvious in the photo. Closer examination reveals that in the blue portion of the stone, the color is lightest at the culet and gradually deepens toward the girdle. This is because the percentage of o-ray in the color gradually increases from 50% at the culet to 100% at the girdle.

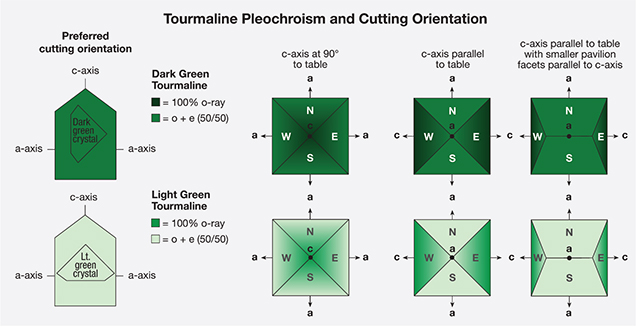
Pleochroism in Tourmaline. Tourmaline is one of the most strongly pleochroic gems. Indeed, its pleochroism is so distinct that it was once used to manufacture crude polariscopes (“tourmaline tongs”). Because of its strong pleochroism, the orientation of cut stones is extremely important (figure 8). In tourmaline, the o-ray is always the darker of the two colors. Thus, light-colored specimens are oriented with the table perpendicular to the c-axis to achieve the richest color. In dark tourmalines the opposite orientation is used, with the c-axis parallel to the table facet. In these stones, the o-ray is so dark that the pavilion facets along the c-axis are typically cut very steep, to minimize the o-ray’s effect on the face-up appearance (figure 9).

Pleochroic Differences in Natural and Verneuil Synthetic Corundum. Differences in the pleochroism of natural and Verneuil synthetic corundum often occur because of differences in their orientation. Natural corundum is generally oriented with the c-axis perpendicular to the table, which tends to provide the best color and weight retention. In the Verneuil product, the c-axis always lies within the plane along which the boule is split. Though not necessarily parallel to the boule’s length, it is always parallel to the plane of the split. As most cutters of this synthetic are only concerned with weight retention—the price is the same regardless of orientation—they will normally place the table facet parallel to the split, so that the c-axis lies parallel to the table. The result is that Verneuil synthetics show dichroism through the table, whereas based on the author’s experience, 80% or more of natural corundum shows little or none (when viewed with a dichroscope).
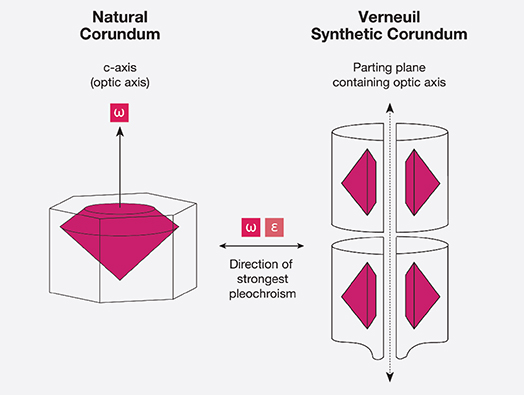
These differences are most readily apparent in blue sapphires and are least conspicuous in yellow to colorless sapphires. Of course, no pleochroism will be detected in completely colorless stones. The differences in the typical orientation of natural and Verneuil synthetic corundum are shown in figure 10. An example of pleochroism in a Verneuil synthetic sapphire boule is shown in figure 11.
It is important to note that in all strongly pleochroic gems cut with the optic axis or axes at oblique angles to the table, the pleochroism, if visible, will have a symmetrical pattern. The different pleochroic colors will be positioned 90° apart from one another, while identical pleochroic colors will lie exactly opposite each other. This is true for both uniaxial and biaxial stones, even if they are cut in a less-symmetrical (e.g., pear or heart) shape. The pleochroism will always be displayed symmetrically because the important optical directions are always arranged symmetrically within the crystal.
PLEOCHROISM IN BIAXIAL GEMS
In biaxial gems, pleochroism is displayed in a manner similar to that of uniaxial gems, except that there are three different pleochroic directions (X, Y, and Z) instead of just two.
Figure 12 shows how the pleochroism of a faceted biaxial gem might vary. Suppose that the color of the X (alpha) vibration direction (not the direction of travel) is cyan, Y (beta) is blue, and Z (gamma) is brown. The gem has been cut with Z perpendicular to the table, X running east-west, and Y running north-south.
- Ray A travels 4 mm parallel to Z, where it vibrates along X and Y, giving 20% X and 20% Y colors. It travels 6 mm parallel to X (vibrating along Y and Z), giving 30% Y and 30% Z. The total of Ray A will consist of 20% X (cyan), 50% Y (blue), and 30% Z (brown).
- Ray B travels 8 mm parallel to Z, where it vibrates along X and Y, giving 40% X and 40% Y colors. It travels 2 mm parallel to X (vibrating along Y and Z), giving 10% Y and 10% Z. The total of Ray B will consist of 40% X (cyan), 50% Y (blue), and 10% Z (brown).
- Ray C travels 4 mm parallel to Z, where it vibrates along X and Y, giving 20% X and 20% Y colors. It travels 6 mm parallel to Y (vibrating along X and Z), giving 30% X and 30% Z. The total of Ray C will consist of 50% X (cyan), 20% Y (blue), and 30% Z (brown).
- Ray D travels 8 mm parallel to Z, where it vibrates along X and Y, giving 40% X and 40% Y colors. It travels 2 mm parallel to Y (vibrating along X and Z), giving 10% X and 10% Z. The total of Ray B will consist of 50% X (cyan), 40% Y (blue), and 10% Z (brown).
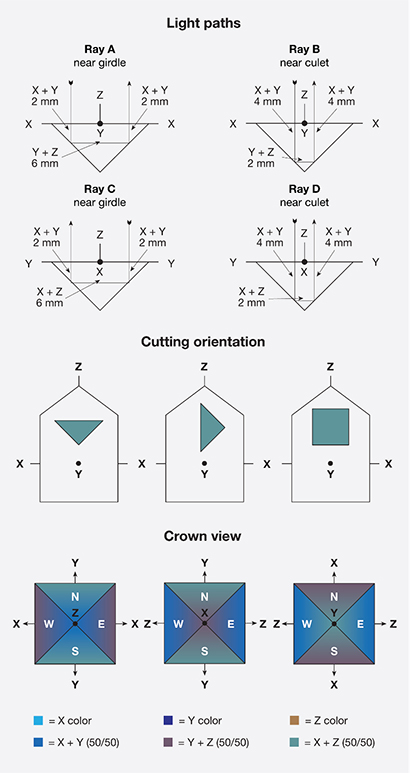
In summary, we can see that biaxial stones have a more complex pleochroism. Facets N and S will show different amounts of the three pleochroic colors compared with facets E and W. As with uniaxial gems, differences in color will be observed not only when comparing facets N and S to facets E and W, but also when comparing areas closer to or farther from the culet on the same facet. These differences are far more complex in biaxial stones, which have three unique vibration directions (compared with only two in uniaxial stones). Keep in mind, however, that differences in color due to pleochroism will occur in a symmetrical pattern, with different pleochroic colors 90° apart from one another, just as in uniaxial gems.
The above descriptions of pleochroism in uniaxial and biaxial gems demonstrate the variation of color on facets of different orientations. But remember that these individual components will mix together to produce the single color seen on any individual point on each facet. A dichroscope can be used to separate that single color into its individual components.
PLEOCHROISM, OR SOMETHING ELSE?
Pleochroism is not the only factor that may cause color variations in faceted gems. Color zoning can result in significant color variations, as can different path lengths of light. Both of these attributes may be present in either singly or doubly refractive gems. Although these should not be confused with pleochroism, they sometimes are.
Consider, for example, an elongated cushion-shaped tsavorite garnet that possesses no visible color zoning (figure 13). With such a stone, the ends of the cushion will appear darker than the sides. This effect could easily be confused with pleochroism, despite the fact that pleochroism cannot occur in singly refractive stones. The actual cause of the darker end facets is the longer light paths.

The Beer-Lambert law states that absorption is directly related to the length of the light path and the concentration of absorbing chromophore. If the path length is doubled while the amount of chromophore remains constant, then the amount of absorption is also doubled. With a 12 mm × 6 mm cushion-cut tsavorite, light internally reflected off the end facets travels down the entire length of the stone, nearly double the path length of light reflected across the side facets. As a result, the end facets are nearly twice as dark as those on the side. If the same piece of rough were cut as a round, however, no variation in color would be seen. Thus, the color variations sometimes seen in singly refractive gems result from variations in light path lengths or color zoning rather than pleochroism.
THE DICHROSCOPE
Not all doubly refractive gems show distinct pleochroism. To determine if color variations across the face of a doubly refractive gem are due to pleochroism or simply variations in path length or color zoning (or even colored inclusions), a dichroscope should be used. Calcite-type dichroscopes (figure 14) are generally preferable to the polarizing types, because calcite is colorless. The polaroid filters used in polarizing dichroscopes generally have a greenish color, which may slightly modify the true pleochroic colors seen, or a grayish color that diminishes the light return.

In using the dichroscope, one must check uniaxial gems at right angles to the c-axis (optic axis) to observe the strongest pleochroism, while biaxial gems should be examined along each of the mutually perpendicular X (alpha), Y (beta), and Z (gamma) directions. But remember that the dichroscope examines transmitted light only. Even if no pleochroism is seen while looking through the table facet, pleochroic color variations may still be visible across the face of a faceted gem (closer to or farther from the culet). This is because the facet orientation causes light to be reflected in more than one direction as it traverses the stone, as previously described.
In doubly refractive stones, color zoning, inclusion color, and path length variations (in non-round or non-square cut shapes) must also be taken into account in determining if visible color variations are due to pleochroism or another factor.
When a faceted colored gem is being examined and described, gemologists need to recognize that the overall appearance perceived as “real” is a synthesis of many factors, some related and some not. Pleochroism is but one. The final determination of pleochroism (and all other color attributes) for purposes of color grading should be made with the gem in the face-up position, as the stone was designed to be viewed. Yet this examination should not be restricted to a direction perpendicular to the table facet. Gems are often viewed at oblique angles, so it seems only logical that the grading should be made in an arc ranging anywhere from parallel to the table to perpendicular to the table.
CONCLUSION
While gemologists typically observe pleochroism with a dichroscope, or possibly a polarizing filter (figure 15), this attribute’s effect on appearance is more complex and generally overlooked. A basic understanding of optical crystallography unlocks the secret of faceted pleochroic gems: When viewing them with the unaided eye, pleochroism is always present, even along an optic axis.

For many gems, pleochroism plays an important role in overall color appearance. It is the wise gemologist and lapidary who understand that this property represents far more than just the twin colors seen in a dichroscope.



