Origin Determination of Dolomite-Related White Nephrite through IB-LDA

ABSTRACT
Provenance studies on nephrite jade are of gemological as well as archeological importance. Origin determination is difficult to achieve relying solely on typical gemological properties and observations. In this study, the authors present a new statistical analysis method, based on linear discriminant analysis (LDA) and trace-element data from laser ablation–inductively coupled plasma–mass spectrometry (LA-ICP-MS), to achieve significantly improved origin determination (an average of 94.4% accuracy) for eight major dolomite-related nephrite deposits in eastern Asia. As the principle is to compare one location to the rest in one round and continue such binary comparison until all possible localities are tested, the method is referred to as iterative-binary LDA (IB-LDA). Combined with trace-element composition data from LA-ICP-MS, it could prove to be a useful technique for the geographic origin determination of other gemstones.
INTRODUCTION
Nephrite jade has been of great interest to East Asian cultures dating back to the Neolithic Age (Wen and Jing, 1996; Tsien et al., 1996; Wen, 2001; Harlow and Sorensen, 2005). Historically, it has been considered a symbol of wealth and power for Chinese emperors and nobility (figures 1A and 1B). Nephrite from countries such as China, Russia, and South Korea (Ling et al., 2013) continues to attract considerable attention as a gem and ornamental material, particularly in the Chinese market. Thus, geographic origin determination is important in terms of proper classification, valuation, and archaeological implications.
In Chinese culture, white is usually regarded as the color of purity and perfection (He, 2009). Due to its quality and well-established historical reputation, white nephrite from Xinjiang has maintained the highest price in the Chinese market. Xinjiang nephrite is usually translucent, with colors ranging from white and greenish white to yellow. The best material from this province is white nephrite with greasy luster, known in the trade as “mutton fat” jade. The purity, fine texture, and luster of white nephrite from Xinjiang come together to create an elegant cultural symbol (figure 1C).
White nephrite from other deposits, including Baikal (Russia), Chuncheon (South Korea), and Qinghai (China), has similar characteristics and is difficult to distinguish with the unaided eye or even microscopic observation (Wu et al., 2002; Ling et al., 2013). In some cases, material from other locations has been falsely represented as Xinjiang nephrite jade to fetch higher prices. A reliable quantitative method for geographic origin determination is urgently needed to protect nephrite consumers.
Nephrite is a gem-quality tremolite or actinolite polycrystalline aggregate. It is usually classified as either dolomite-related or serpentine-associated, which have different formation processes and different concentrations of Fe, Cr, Co, and Ni, as well as oxygen and deuterium isotopes (Yui and Kwon, 2002; Harlow and Sorensen, 2005; Siqin et al., 2012; Adamo and Bocchio, 2013). Dolomite-related nephrite is usually white, greenish white, yellow, or light gray, due to the relatively low concentrations of the transition metal elements listed above. Serpentine-associated nephrite is usually green. A typical example is Siberian green nephrite from Russia, known for its purity of color. The geographic sources of serpentine-associated nephrite, such as New Zealand, mainland China, and Taiwan, can be distinguished by some characteristic elements in chromite inclusions and by strontium isotopes (Adams et al., 2007; Zhang and Gan, 2011; Zhang et al., 2012).
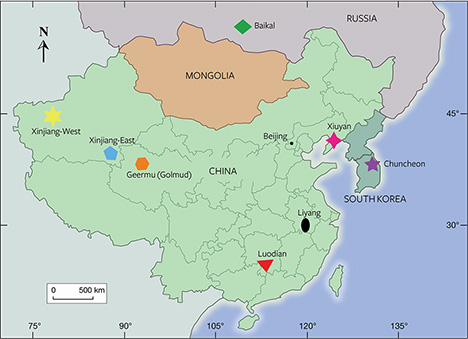
There is no widely accepted method for distinguishing the geographic origin of dolomite-related nephrite. Two factors account for this. First, there are many sources for dolomite-related nephrite in East Asia. Eight major locations are listed in figure 2: western Xinjiang (including the famous Hetian area) and eastern Xinjiang province (China); Geermu, also known as Golmud (Qinghai province, China); Xiuyan (Liaoning province, China); Luodian (Guizhou province, China); Liyang (Jiangsu province, China); Baikal (Russia); and Chuncheon (South Korea). Second, because of their similar standard gemological properties, such as color, transparency, luster, refractive index, specific gravity, and major element components (Liao and Zhu, 2005; Ling et al., 2013; Liu and Cui, 2002), dolomite-related nephrite jades from these locations are very difficult to distinguish.
Geochemical research has shown that trace elements can reflect the sources of gemstones (Breeding and Shen, 2010; Blodgett and Shen, 2011; Shen et al., 2011; Zhong et al., 2013). But as the number of producing localities and the complexity of chemical composition increase, simply evaluating one or two elements cannot distinguish the different origins (Siqin et al., 2012). Multiple elements, and correlations between those elements, must be taken into account. Identifying and optimizing the variables that characterize differences among origins becomes the main focus.
Linear discriminant analysis (LDA) is a popular statistical method that can reduce the multiple dimensions of variables and provide reliable classification accuracy (Fisher, 1936; Yu and Yang, 2001; McLachlan, 2004; Guo et al., 2007). Recently, this method has been used to identify the geographic origins of some single-crystal gemstones such as Paraíba tourmaline, ruby, sapphire, and peridot (Blodgett and Shen, 2011; Shen et al., 2013).
In this work, the trace-element composition and distribution of 138 dolomite-related nephrite samples from the major producing areas in East Asia have been carefully summarized. Based on the trace-element data, we propose an algorithm, which we refer to as iterative binary LDA (IB-LDA), to achieve nearly complete separation of the dolomite-related nephrite deposits. This method may have wide-ranging applications for additional mineral and gemstone origin research in the future.
MATERIAL AND METHODS
Sample Preparation. All samples in this study were collected directly from the mines in eight major East Asian dolomite-related nephrite jade deposits. A total of 138 samples, with 15–19 specimens from each locality (see table 1), were chosen for LA-ICP-MS testing.
| TABLE 1. Dolomite-related nephrite samples used in this study. | |||||
| Labeled | Locations | Mining area sources |
Quantity
(total 138)
|
LA-ICP-MS
test points
(total 452)
|
Main color |
| 1 | Xinjiang-West | West of Xinjiang province, China; includes Hetian, Yecheng, Xueyanuote, Xinzang 383, and Datong |
17 | 60 |
White to greenish
white |
| 2 | Xinjiang-East | East of Xinjiang province, China; includes Qiemo and Ruoqiang |
18 | 60 | White to light greenish white |
| 3 |
Geermu
(Golmud)
|
Qinghai province, China | 17 | 60 | White to light greenish white |
| 4 | Baikal | Russia | 17 | 60 | White |
| 5 | Chuncheon | South Korea | 21 | 60 | White |
| 6 | Xiuyan | Liaoning province, China | 17 | 60 | White to caramel |
| 7 | Luodian | Guizhou province, China | 15 | 60 | White |
| 8 | Liyang | Jiangsu province, China | 16 | 32 | Greenish white |
The samples were cut into blocks measuring 3.0 × 1.5 × 0.5 cm (length × width × height). The bodycolor ranged from white to light greenish, with scattered colors such as yellow in some samples. Samples with representative color from each deposit are shown in figure 3.

On each nephrite block, three to five points along a straight line with 5 mm intervals between each point were selected for LA-ICP-MS testing; see the “LA-ICP-MS Measurement” section below. We collected 60 test points for each origin for further statistical analysis, to be discussed in the “LDA Method” section. Due to the heterogeneous chemical composition of polycrystalline nephrite and the relatively limited number of block samples (only 15–19 per each origin), we treated each test point as an independent sample, so that each origin has a data set of 60 analyses.
LA-ICP-MS Measurement. Trace-element concentrations of the 138 samples were measured using an LA-ICP-MS system at the State Key Laboratory of Geological Processes and Mineral Resources, China University of Geosciences, Wuhan. The LA-ICP-MS system consisted of a GeoLas 193 nm laser and an Agilent 7500 ICP-MS. The laser fluence was set as 10 J/cm2, and the ablation spot size was 32 µm. The widely used quantitative calibration standards of NIST synthetic glasses SRM610 (Pearce et al., 1997) and U.S. Geological Survey (USGS) synthetic glasses of BCR-2G, BHVO-2G, and BIR-1G (Jochum et al., 2005) were used as reference materials. Three to five spots on each sample, at approximately 5 mm intervals along a straight line, were collected for analysis. 29Si was used as an internal standard. Detailed operating conditions for the laser ablation system and the ICP-MS instrument and data reduction were the same as those described by Liu et al. (2008, 2010).
LDA Method. Linear discriminant analysis is the primary tool in this classification of nephrite from dolomite-related deposits. This method was designed for group classification, which aims to maximize between-class variance while minimizing within-class variance. Free software utilizing the statistical programming language R, version 3.1.2, was applied to this statistical analysis. Based on the trace-element concentrations collected using LA-ICP-MS, the general procedure for LDA origin determination entailed two steps. First, original data sets of 40 independent test points for each origin except Liyang (which has a distinguishable feature, to be explored in the Discussion section), along with their trace-element information, were treated as “training sets” to build the discriminant functions (DFs) and find the best separation. The validity of the separation is characterized by the eigenvalue (EV) and total cross validation (CV); see box A for detailed definitions of EV and CV. Second, four additional samples from each origin, along with their trace-element information, were treated as test sets. The purpose of a test set is to estimate how the classification model will deal with the data that was not included in the “training set” to build the DFs. As conventional settings for machine learning models (Kohavi, 1995), two-thirds of the total data sets (280 data points) were used as a training set, and one-third (the other 140 data points) were used as test set. This setting applies throughout the paper unless other specific modifications are mentioned. Detailed descriptions of training sets and test sets also appear in box A.
RESULTS AND DISCUSSION
For the 138 nephrite samples from the eight locations, the concentration of elements from Li to U (45 elements total) were obtained by LA-ICP-MS measurement. To make our classification model independent of sample color, the transition metal elements (Ti, V, Cr, Mn, Fe, Co, Ni, and Cu) were excluded from further data analysis. Only 34 trace elements were involved in creating the LDA model. The mean value and standard deviation value of each trace element are calculated based on 60 detection points for each origin, as shown in table 2.
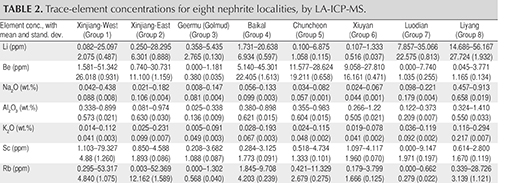
Trace-Element Analysis to Separate Liyang from Other Origins. As shown in table 2, the nephrite samples from Liyang (group 8) displayed much higher concentrations of Sr (>140 ppm) and Na2O+K2O (>0.57 wt.%) than the other seven localities (Sr<40 ppm, Na2O+K2O < 0.56 wt.%). These results confirmed previously reported conclusions (Zhang et al., 2011; Siqin et al., 2012; Ling et al., 2013) that the distinctive Sr, Na, and K concentrations could be used as a quantitative discriminant to separate Liyang nephrite samples. These obvious diagnostic chemical signatures rendered further analysis of Liyang nephrite unnecessary. The only real challenge was to distinguish the remaining seven nephrite origins. Table 2 shows overlapping trace-element distributions. Therefore, it is important to derive effective discriminants from the trace elements to separate the origins.
Traditional LDA in Dolomite-Related Nephrite Origin Determination. From the outset, we attempted to use the traditional LDA method to classify the seven dolomite-related nephrite localities at once. Each nephrite locality is classified as a group, and every input trace element represents an independent variable. Seven linear discriminant functions (DFs) for seven independent nephrite groups were built simultaneously. The results showed that only the Luodian samples had an isolated distribution region, while the other six localities still exhibited overlap. The full classification of all seven groups by “one-pass” LDA must balance variance among all seven groups. This may be the reason why traditional LDA presented a relatively low CV of 91.4 % and a relatively low EV of 4.48 with a training set size of 40 testing points for each group. For the details of DFs and CV, again see box A.
IB-LDA to Optimize the Separation of Dolomite-Related Nephrite Geographic Origins. If only aiming to distinguish one group from all the others while ignoring the differences within the remaining unclassified groups, certain group identities should be more accurate and distinguishable. Hence, we designed the “iterative-binary” LDA (IB-LDA) to optimize the separation. The procedure used to build the discriminant function and criteria database for all seven origins is described in box A.
Classifying different sources of dolomite-related nephrite by IB-LDA is analogous to sorting blocks with different shapes by putting them into the corresponding holes. As shown in figure 4, seven blocks represented seven different dolomite-related nephrite origins. The red triangle, pink four-pointed star, purple five-pointed star, yellow six-pointed star, green square, blue pentagon, and orange hexagon represented Luodian, Xiuyan, Chuncheon, Xinjiang-West, Baikal, Xinjiang-East, and Geermu (Golmud) respectively. We then needed to build corresponding blocks with differently shaped holes (named “chosen sieves” hereafter) using the training set samples. The original 280 training set samples from the seven origins were used to create seven chosen sieves in sequence after six rounds of IB-LDA processes (figure 4). The different holes represent different DFs built for each chosen sieve. The sequence of those chosen sieves directly corresponds to the six rounds of IB-LDA, which must be unchanged to maintain the validity of the classification method. We found that the IB-LDA model produces better CV and EV values than traditional LDA, as shown in table A-1, which indicates IB-LDA can effectively improve the accuracy and validity of the sieves (classification model).

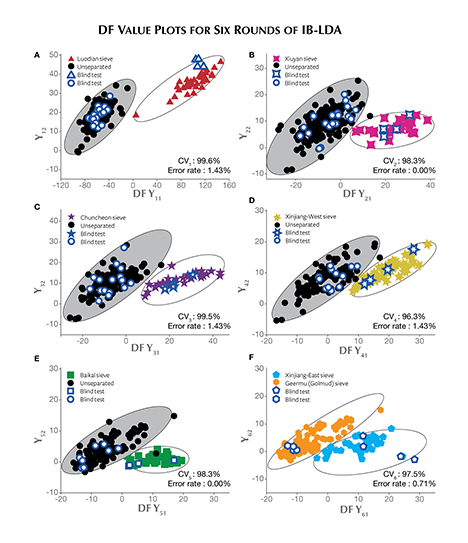
Next, we evaluated the performance of the sieves built by IB-LDA on unincluded data in a blind test. Four new samples from each origin were used as a testing set to check the reliability and accuracy of the established chosen sieves (figure 5). All samples were treated as “unknown” blocks to be tested on the seven sieves in sequence. When the unknown block fit into the correct sieve, its “shape” was identified. For example, the first chosen sieve (Luodian) allowed only the triangular blocks to be sorted out, which meant only Luodian samples could be identified and all the other samples were still in an “unseparated” status. The unseparated samples went through the second IB-LDA process, where a four-pointed star sieve representing Xiuyan was used to extract appropriately shaped blocks, and the unseparated pool was reduced once more.
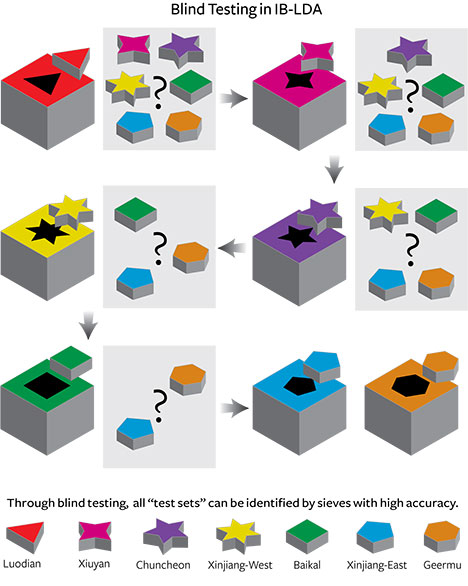
This process should be repeated until all the unseparated blocks can be identified. The number of test sets with the correct classification divided by the number of the total test sets is the accuracy rate (AR) for such blind testing. The same blind test is performed five times on different test sets, and the average AR is calculated. We note that the AR value obtained is generally consistent with the CV value calculated in the first step of IB-LDA, as shown in table A-1.
CONCLUSIONS
We propose that an IB-LDA model, combined with trace-element information from LA-ICP-MS, is an effective method for determining the origin of dolomite-related nephrite deposits. We consider the application of IB-LDA to the quantitative classification of nephrite origin a significant improvement over the traditional method. The origin information reflected by trace-element data has been well explored and applied in nephrite origin determination. The LDA method presents obvious statistical advantages in dealing with the massive quantity of nephrite trace-element data. Finally, the successful performance of IB-LDA remarkably improved discriminant accuracy, increasing the CV accuracy rate from 91.4% in traditional LDA to 94.4% and identifying CVorNi values specific to each origin. The discriminant functions database built by IB-LDA obtained a 95.0% accuracy rate in the testing of 28 unknown samples. We believe that collecting and accumulating more nephrite samples for use as training sets will further improve the reliability of the discriminant function database. The IB-LDA method should also prove useful for the origin determination of other gemstones.
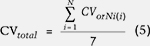

.jpg)


