The Role of Silicon in the Color of Gem Corundum
ABSTRACT
Natural corundum is colored by a variety of trace-element impurities and by the chemical reactions among them. Important to nearly all of the colors is the role played by the reactions among silicon, titanium, and magnesium. Characterization of the interactions between these aliovalent ions has been hindered by the fact that the laser ablation–inductively coupled quadrupole–mass spectrometry equipment used in most gem labs does not resolve the interferences for silicon. Thus Si has not been measured at relevant concentrations. Recent development of ion implant standards and the application of secondary ion mass spectrometry has allowed the accurate measurement of silicon in corundum for the first time. As an example of its importance, detailed analyses of sapphire from Montana’s Yogo Gulch deposit are presented. These analyses show that without silicon, Yogo sapphire would not be blue.
INTRODUCTION
Corundum, like many other transparent gemstones, is inherently colorless if pure. In fact, pure corundum has an excellent transmission window that can achieve good transparency between approximately 0.18 and 5 µm (Khattack and Schmid, 2001). Pure corundum is aluminum oxide, Al2O3. Thus, the only cation (positive ion) in pure corundum is Al3+ and the only anion (negative ion) is O2–. Neither of these two ions arrayed in the corundum lattice structure absorbs light in the visible region of the spectrum. The color of corundum gems is therefore determined by trace element impurities that are in solution in the corundum lattice. Such gems are referred to as allochromatic (“other colored”).
“In solution” is an important distinction to make. Sugar dissolved in water is “in solution.” Fine sand stirred into water is not. “In solution” in corundum means that if the impurities are cations, they will primarily substitute for Al3+ in the corundum lattice. If they are anions, they will primarily substitute for O2– in the corundum structure.
This paper discusses how trace elements chemically interact with each other, and thus concentrations will be expressed as atomic concentrations in units of parts per million atomic (ppma), not weight concentrations (ppm or ppmw). These units are chosen because it is the concentration of trace elements that determines how they chemically interact, not their relative weights.1
Al3+ is one of the smallest trivalent cations, with a radius of only 53 picometers (pm; 1 pm = 10–12 m) in sixfold coordination, which means six oxygen ions surround a single aluminum ion. This cation site in corundum is quite small, limiting the size and thus the variety of trace elements that can be easily incorporated. Whereas corundum has only a single small cation site, other gems (beryl, for example) can have multiple cation sites of different sizes.
For trivalent cations substituting for Al3+ at geologic temperatures, size is the primary factor in determining the solubility (Blundy and Wood, 2003; Karato, 2016). Trivalent ions in corundum are termed isovalent (same valence). Isovalent ions that are larger than aluminum stretch the lattice. The energy required to stretch the lattice results in a reduced solubility. Isovalent ions that are smaller than Al3+ also create substantial lattice distortion that reduces solubility.
Cations in corundum with a valence different than the +3 of aluminum are termed aliovalent (different valence). Since a solid must be rigorously electrically neutral, the incorporation of an aliovalent trace element requires either the incorporation of another aliovalent ion to achieve an average charge of +3 for the pair, or the creation of a charged crystal defect such as an interstitial ion, a vacancy, or a change in valence of an existing ion. These requirements are energy intensive and result in very low solubilities for aliovalent ions as compared to isovalent ions of the same size (Blundy and Wood, 2003).
The overall result of size and valence constraints in corundum is that in nature only a small fraction of the elements in the periodic table are found in solution. The majority of these elements are listed in table 1, along with their radii in the sixfold coordination of corundum.
| TABLE 1. Radii of selected elements found in natural corundum.a | ||
| Cation | Valence | Ionic radii (pm) |
| Berylliumb | +2 | 45 |
| Magnesium | +2 | 72 |
| Aluminum | +3 | 53.5 |
| Nickel | +3 | 56 |
| Iron | +3 | 55 |
| Manganese | +3 | 58 |
| Chromium | +3 | 61.5 |
| Gallium | +3 | 62 |
| Vanadium | +3 | 64 |
| Silicon | +4 | 40 |
| Titanium | +4 | 60.5 |
|
aData from Shannon (1976) and Dyar and Gunter (2008)
bBeryllium is often found in natural corundum, but it is associated with inclusion clouds. Whether Be exists in solution is not yet clear. |
||
The foregoing rules are useful for growth of corundum at low temperatures, such as in geologic growth. However, it should be pointed out that for growth from a corundum melt at 2050°C (Czochralski, Verneuil, etc.), other factors can modify these general rules.
The trace elements in corundum chemically interact with each other, and this interaction is, in many cases, key to the resulting color we observe. In Emmett et al. (2003), this interaction and the resulting colors produced were discussed at length. Rather than recreate that discussion here, the reader is referred to that paper. However, as presented in that paper, the chemical reaction among trace elements is based on their relative energy level positions in the band gap as shown in figure B-1 in Emmett et al. (2003). The positions shown were based on a summary paper (Kröger, 1984a). That paper shows that the silicon donor level lies well below the titanium donor level, and we used that position in our analysis of the effect of silicon on the color of corundum.
Unknown at the time was that a second summary paper by the same author (Kröger, 1984b) corrected the silicon donor level based on measured data in a concurrent paper by Kröger and one of his students (Lee and Kröger, 1985). These later two publications clearly show that the correct silicon donor level lies well above the titanium donor level. The second summary paper also corrects the relative level positions of some of the transition metals. Figure 1 of this paper presents data from the second summary paper and clearly shows that the silicon donor level is well above the titanium donor level.
While the position of the silicon donor level with regard to the position of the titanium donor level may seem unimportant, it surely is not. Their relative positions have a significant impact on how trace elements react with each other, and in certain cases it is only the presence of silicon that allows the titanium to pair with iron, creating the blue coloration of the Fe2+-Ti4+ pair in sapphire.
To understand how this comes about, we need to examine the corrected band gap chart in figure 1. This is a greatly simplified version of the correct chart from Kröger (1984b). The convention of labeling these levels is to show the donor level before donating an electron (e.g., Ti as Ti3+), and the acceptor levels after accepting the electron (e.g., Fe as Fe2+). As such, the vertical distance between the donor and acceptor states is a measure of the binding energy of the donor-acceptor pair.
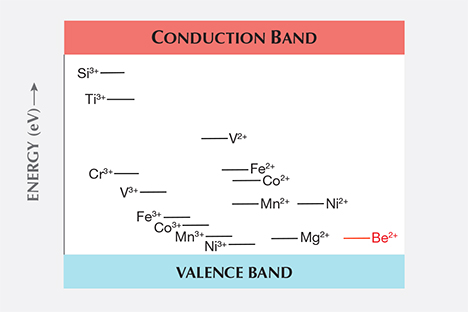
The beryllium acceptor level in figure 1 is shown in red, as it was not presented in Kröger (1984b) and has not been accurately measured. It is estimated from the original beryllium diffusion experiments (Emmett et al., 2003).
From the defect chemical reactions and energy level positions, we can formulate a series of rules about impurity interactions (Smyth, 2000). These rules will not be valid for all concentration levels or all temperatures. They become less valid as concentrations of key elements (such as Mg, Si, and Ti) exceed a few hundred ppma or at temperatures substantially above room temperature. A correct formulation requires solving the equilibrium chemical defect reactions for all of the impurities simultaneously, but measurements of the equilibrium constants for all the reactions are unavailable. However, the following rules are useful for a wide variety of situations and, more importantly, will serve to illustrate the types of chemical reactions that occur among impurities in corundum. These rules correct those presented in Emmett et al. (2003), written when it was believed that the silicon donor level was below that of titanium.
- If there are two acceptors and a single donor, the lowest acceptor preferentially pairs with the donor unless both acceptors are energetically close together in the band gap, in which case the donor will pair with both.
- If there are two donors at different levels and a single acceptor, the highest donor will preferentially pair with the acceptor. If the two donor energy levels are energetically close together in the band gap, they will both take part in charge compensation of the acceptor.
- If corundum contains Ti, Mg, and Fe, Ti will pair with Mg before Fe.
- If corundum contains Si, Mg, and Fe, Si will pair with Mg before Fe.
- If corundum contains Si, Ti, Mg, and Fe, Si will pair with both Mg and Fe before Ti will.
- When the concentration of Mg exceeds the sum of both Si and Ti, the excess Mg will be charge compensated by trapped holes (see Emmett et al., 2003, p. 92) in oxidizing conditions, or by oxygen vacancies under reducing conditions, or by both.
Why are we still uncertain about the role of silicon in corundum? We certainly understand the roles of Ti, Fe, and Mg. It is because we have not been able to measure the silicon content of the sapphire samples we have studied. The instruments used for laser ablation–inductively coupled plasma–quadrupole mass spectrometry (LA-ICP-QMS) in use in most laboratories show significant interferences for the three silicon isotopes. Thus, when a very high-purity sample of synthetic sapphire is measured on these instruments, it shows nominally several tens to several hundreds of ppma silicon that is not there (Shen, 2010). The reason for this is that in the plasma, small quantities of unusual molecules are formed with a mass close to that of silicon; these molecules are recorded by the instrument as silicon. For example, 28Si is the most abundant isotope of silicon, at 92.23% abundance. Its mass is 27.97693 atomic mass unit (amu). When ablating corundum, aluminum carried by the plasma can combine with hydrogen from even a miniscule amount of water vapor to form 27AlH with a mass of 27.98936. The mass difference between 28Si and 27AlH is only about 4 parts in 10,000, which is too small for the instrument to resolve, and so the instruments record both as silicon. The mass resolution of quadrupole mass spectrometers used in normal gemological laboratories at mass 28 is only 2–3 parts in one hundred in the normal resolution mode, and only about 1 part per hundred in the high-resolution mode. The required resolution of 4 parts in 10,000 far exceeds the capability of a commercial “desktop” design ICP-QMS in normal gemological laboratories. High-resolution QMS is not available commercially. This example dramatically shows why a zero trace element concentration, matrix-matched standard is critical for the interpretation of data from these and other analytical instruments. Similar interferences have been measured for the other two silicon isotopes (Shen, 2010).
A few years ago, GIA initiated a project to develop an improved set of matrix-matched standards for the analysis of corundum with the existing LA-ICP-QMS instruments. The approach was to make ion implant standards in sapphire for each element of interest and calibrate them with Rutherford backscattering spectrometry (RBS). For those trace elements lighter than or close in mass to aluminum (i.e., Be, Mg, and Si), secondary ion mass spectrometry (SIMS) was used against multiple highly characterized standards kept by Evans Analytical. With calibrated ion implant standards, the next step was to grow multi-element doped sapphire crystals for the laboratory standards, which was done by Scientific Materials Corporation. The calibration was then transferred from the ion implant standards to the multiply doped crystals with Caltech’s SIMS facility (GIA, 2016). A silicon ion implant standard was also prepared with the hope that advanced instrumentation would eventually allow the analysis of silicon.
The plan for the standards was to have a three-point calibration—a zero, a mid-range value, and a high value for each element. Sapphire crystals were grown that accomplished these goals except for the high-range iron value. Iron and its oxides all have high vapor pressure at the Czochralski growth temperature (~2300°C) and thus distill out of the melt.
All of the multi-element doped crystals were calibrated at the SIMS facility against the ion implant standards. When the extremely high-purity sapphire crystal (the zero standard) was measured by SIMS, it demonstrated that SIMS could resolve the isotopic interferences for silicon. SIMS could therefore measure silicon in corundum samples against an ion implant standard.
To create a high-range iron standard, a different approach had to be employed. Natural sapphires from Montana’s Yogo deposit (figure 2) were evaluated for uniformity. The Yogo sapphire is almost unique for the extreme uniformity of its blue color, which indicates a high trace element concentration uniformity, at least for the Fe2+-Ti4+ chromophore. A typical sample is shown in figure 3. It was hoped that this uniformity would also extend to Fe3+. The SIMS analyses of nine pieces of Yogo sapphire at nine points each did show a very high iron uniformity, and thus it was chosen to be the high iron concentration standard. The nine Yogo samples were calibrated with SIMS for all elements for which ion implant standards had been prepared. Since we can easily resolve the mass interference for silicon in corundum using the high mass resolving power of SIMS, accurate silicon measurements of natural corundum samples have been obtained for the first time.


Surprisingly, it also turned out that the Yogo sapphires provided an excellent example of the role of silicon in gem corundum. The trace element concentrations and color are extremely uniform, and thus the standard deviations (SDs) of the concentration measurements are quite small. SIMS analysis of the individual trace elements against corundum ion implant standards is shown in table 2. The data presented are the average of three measurement points on this particular sample.
| TABLE 2. SIMS analysis of a typical Yogo sapphire sample (in ppma). | |||||||||
| Trace elements | Mg | Si | Mg – Si = available Mg |
Ti | Ti – available Mg = available Ti |
V | Cr | Fe | Ga |
| Concentration | 84.3 | 24.6 | 59.7 | 79.7 | 20.0 | 2.7 | 2.2 | 1130 | 10.4 |
| Standard deviation (ppma) |
1.32 | 0.44 | 1.4 | 0.72 | 1.6 | 0.05 | 0.08 | 20 | 0.3 |
Since Si is the highest-lying donor and Mg the lowest-lying acceptor, Si will pair with Mg first, leaving 59.7 ppma Mg2+ available to interact with other trace elements. Then Ti as a donor will pair with all the remaining available Mg, leaving 20.0 ppma Ti to pair with Fe, producing the blue coloration. It is interesting to note that without silicon, Yogo sapphire would not be blue because Mg > Ti, and thus no unpaired Ti would be available to pair with Fe. The analysis of this Yogo sapphire is not unusual but is typical of all of the Yogo samples analyzed.
This clearly demonstrates the critical role of silicon in the color of corundum, a factor that, to the best of our knowledge, has not been correctly addressed in the literature.
The SDs presented in table 2 only relate to the point-to-point analysis variations of the sample. For determining the SDs of the absolute measurement, it is necessary to correctly combine the point-to-point SDs with the SDs of the ion implant standards. When this is done, the SD result for the “available titanium” becomes 6.7 ppma, which is well below the stated concentration value of 20 ppma. While this addition to the SD is rarely applied in the gemological literature, it is presented here to emphasize the validity of the absolute result.
The SIMS analysis of Si conducted on nine Yogo samples resulted in Si concentrations from 22 to 26 ppma. In addition, ten other samples from Myanmar, the Rock Creek deposit in Montana (United States), the Garba Tula deposit in Kenya, the Subera deposit in Queensland (Australia), the Pailin deposit in Cambodia, and the Montepuez ruby deposit in Mozambique were also analyzed for silicon. The concentrations measured ranged from 3.5 to 150 ppma. In each case the silicon concentration was in the same range as the concentrations of the other aliovalent ions, and thus in each case it had a significant impact on color.
CONCLUSIONS
It is clear from the foregoing study that silicon is an important trace element in gem corundum, contributing substantially to the resulting color. The current analytical capabilities of most of the world’s gem labs do not allow the quantification of silicon at relevant concentration levels. Consideration should be given to the possibility of obtaining higher-resolution mass detectors for the existing LA-ICP equipment, or to evaluating other analytical techniques such as laser-induced breakdown spectroscopy (LIBS).
FOOTNOTES
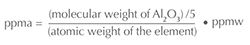
.jpg)


